Geometry - Quantitative Aptitude

Q11. An angle is two-third of its supplement. The measure of the angle is
(a) 30⁰
(b) 45⁰
(c) 58⁰
(d) 72⁰

Q12. In the given figure, straight lines AB and CD intersect at O. If ∠x = 3∠y, then ∠y = ?
(a) 20⁰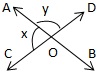
(b) 40⁰
(c) 45⁰
(d) 60⁰

Q13. Two supplementary angles are in the ratio 2 : 4. The smaller angle measures
(a) 45⁰
(b) 60⁰
(c) 75⁰
(d) 90⁰

Q14. An angle is 20⁰ more than its complement. The measure of an angle is
(a) 55⁰
(b) 65⁰
(c) 70⁰
(d) 73⁰

Q15. How many angles are made by 5 rays shown in the figure ?
(a) 5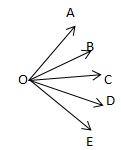
(b) 7
(c) 10
(d) 12

Q16. In the given figure, l₁ || l₂ and ∠A = 70⁰, then ∠C = ?
(a) 60⁰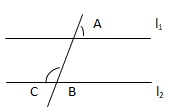
(b) 90⁰
(c) 110⁰
(d) 125⁰

Q17. In the given figure, ∠AOD = 90⁰. What is the measure of ∠COB.
(a) 45⁰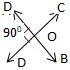
(b) 90⁰
(c) 105⁰
(d) 180⁰

Q18. In the given figure, AOB is a straight line, ∠AOC = (5x + 10)⁰, ∠BOC = (3x - 22)⁰, the value of x is
(a) 24⁰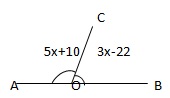
(b) 27⁰
(c) 35⁰
(d) 38⁰

Q19. If Δ PQR is an isosceles triangle with ∠R = 90⁰ and RQ = 6 cm, then PQ = ?
(a) 4√2 cm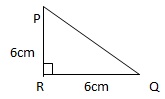
(b) 6√2 cm
(c) 7√2 cm
(d) 9√2 cm

Q20. In a cyclic squad ABCD, ∠A = 70⁰, then ∠C = ?
(a) 60⁰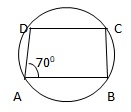
(b) 90⁰
(c) 105⁰
(d) 110⁰

___________________________________________________________________________