Trigonometry - Quantitative Aptitude
Q1. If Sinθ = 1/√2 and Cosθ = 1/√3, then tanθ = ?
(a) √3/√2
(b) √2/√3
(c) √5/√3
(d) √3/√5
Answer: (a) √3/√2
| tanθ = | Sinθ | = | 1/√2 | = | √3 |
| Cosθ | 1/√3 | √2 |
Q2. If tanθ = 3/5 and θ is avute angle the Cosecθ = ?
(a) √23/√2
(b) √29/√2
(c) √34/√3
(d) √37/√5
Answer: (c) √34/√3
We have
Cosecθ = √1 + Cot2θ = √ 1 + 1/tan2θ
| = √ | tan2θ + 1 | = | √ tan2θ + 1 | = | √ 1 + (3/5)2 | = | √ 1 + (9/25) | = | √ 34/25 | = | 5√ 34 | = | √ 34 |
| tan2θ | tanθ | 3/5 | 3/5 | 3/5 | 3 X 5 | 3 |
Q3. If Sinθ = √3/2, then the value of 2(Cosecθ + Cotθ) = ?
(a) 2√3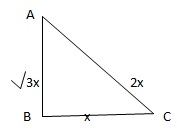
(b) 2√5
(c) 3√2
(d) 5√3
Answer: (a) 2√3
Sinθ = √3/2 = √3x/2x = AB/AC
Now AC2 = AB2 + BC2
⇒ BC = √AC2 - AB2 = √4x2 - 3x2 = x
| Cosecθ = | AC | = | 2 |
| AB | √3 |
| Cotθ = | BC | = | x | = | 1 |
| AB | √3x | √3 |
| ∴ 2(Cosecθ + Cotθ) = 2 ( | 2 | + | 1 | ) = 2 ( | 3 | ) = 2√3 |
| √3 | √3 | √3 |
Q4. (5π/6) radians = ?
(a) 1200
(b) 1500
(c) 1800
(d) 2200
Answer: (b) 1500
(5π/6) radians = 5/6 X 1800 = 1500
Q5.
| 1 | + | 1 | = ? |
| 1 + tan2θ | 1 + Cot2θ |
(a) 1
(b) 3
(c) 4
(d) 5
Answer: (a) 1
| 1 | + | 1 | = | 1 | + | 1 | = Cos2θ + Sin2θ = 1 |
| 1 + tan2θ | 1 + Cot2θ | Sec2θ | Cosec2θ |
Q6. The maximum value of (Sinθ + Cosθ) is
(a) √2
(b) √3
(c) √4
(d) √5
Answer: (a) √2
(Sinθ + Cosθ) is maximum when θ = 450
∴ Sin450 + Cos450 = 1/√2 + 1/√2 = 2/√2 = √2 . √2/√2 = √2
Q7. If xSin2600 - ½ Sec600tan2300 + 4/3Sin2450tan2600 = 0, then x2 = ?
(a) 200/61
(b) 300/71
(c) 350/79
(d) 400/81
Answer: (d) 400/81
xSin2600 - ½ Sec600tan2300 + 4/3Sin2450tan2600 = 0
⇒ x. (√3/2)2 - ½ X 2 X (1/√3)2 + 4/3 X (1/√2)2 X (√3)2 = 0
⇒ x. ¾ - 1/3 + 4/3 X ½ X 3 = 0
⇒ 3x/4 - 1/3 + 2 = 0
| ⇒ | 9x - 4 + 24 | = 0 |
| 12 |
⇒ 9x + 20 = 0
⇒ x = -20/9
⇒ x2 = (-20/9)2 = 400/81
Q8. 3Sin2300 - 3Cos2450 + 3tan2600 = ?
(a) 31/3
(b) 33/4
(c) 37/7
(d) 39/11
Answer: (b) 33/4
3Sin2300 - 3Cos2450 + 3tan2600
= 3 X (½)2 - 3 X (1/√2)2 + 3 X (√3)2
| = 3 X | 1 | - 3 X | 1 | + 3 X 3 |
| 4 | 2 |
| = | 3 | - | 3 | + 9 |
| 4 | 2 |
| = | 3 - 6 + 36 | = | 33 |
| 4 | 4 |
Q9. If Cosθ = 5/13 , 0 ∠ θ ∠ π/2, then (Cosθ + 5Cotθ)/(Cosecθ + Cosθ) = ?
(a) 375/221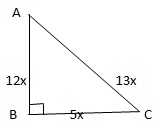
(b) 385/229
(c) 392/321
(d) 399/339
Answer: (b) 385/229
| Cosθ = | 5 | = | 5x | = | BC |
| 13 | 13x | AC |
Now AB = √AC2 - BC2
= √(13x)2 - (5x)2
= √169x2 - 25x2
= √144x2 = 12x
| Now | Cosθ + 5Cotθ | = | 5x/13x + 5 X (5x/12x) | = | 5x/13x + 25x/12x | = | 60 + 325 | = | 385 |
| Cosecθ + Cosθ | 13x/12x + 5x/13x | 13x/12x + 5x/13x | 169 + 60 | 229 |
Q10. If tan2450 - Cos2600 = xSin450Cos450tan600, then x2 = ?
(a) 2/3
(b) 2/5
(c) 3/5
(d) 3/7
Answer: (c) 3/5
tan2450 - Cos2600 = xSin450Cos450tan600
⇒ 12 - (½)2 = x. 1/√2. 1/√2 X √3
⇒ 1 - ¼ = √3 x/2
| ⇒ | 3 | = | √3x |
| 4 | 2 |
| ⇒ x = | 3 | X | 2 | = | 3 | = | √3 . √3 | = | √3 |
| 4 | √3 | 2√3 | 2√3 | 2 |
⇒ x2 = (√3/2)2 = 3/4

Practice Test Exam