Trigonometry - Quantitative Aptitude
Q11. The angle of elevation of a tower from a distance 100m from its foot is 300. The height of the tower is
(a) 65/√2 m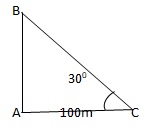
(b) 75/√2 m
(c) 90/√3 m
(d) 100/√3 m
Answer: (d) 100/√3 m
Let, AB be the height of the tower.
Let AC = 100 m, ∠ACB = 300
| Now tan300 = | AB |
| AC |
| ⇒ | 1 | = | AB |
| √3 | 100 |
| ⇒ AB = | 100 | m |
| √3 |
Q12. At an instant, the length of the shadow of a pole is √3 times the height of the pole. The angle of the elevation of the sun is
(a) 300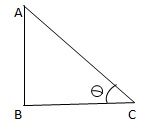
(b) 450
(c) 600
(d) 900
Answer: (a) 300
Let, the height of the pole be AB and angle of elevation be θ
∴ length of shadow BC = AB. √3
| ∴ tanθ = | AB | = | AB | = | 1 | = tan300 |
| BC | √3 AB | √3 |
∴ θ = 300
Q13. The angles of depression of two ships from the top of a light house are 450 and 300 towards east. If the ships are 100 m apart, the height of the light house is
(a) 20(√2 + 1)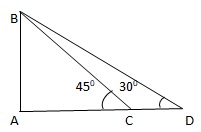
(b) 30(√3 + 1)
(c) 40(√2 + 1)
(d) 50(√3 + 1)
Answer: (d) 50(√3 + 1)
Let, AB be the light house and C and D be the positions of the ships such that CD = 100 m
∠ACB = 450, ∠ADB = 300
| tan450 = | AB |
| AC |
| ⇒ 1 = | AB |
| AC |
⇒ AB = AC
| Now | AB | = tan300 = | 1 |
| AD | √3 |
| ⇒ | AB | = | 1 |
| AC + CD | √3 |
| ⇒ | AB | = | 1 |
| AC + 100 | √3 |
⇒ AB + 100 = AB√3
⇒ AB(√3 - 1) = 100
| ⇒ AB = | 100 | = | 100 (√3 + 1) | = | 100 (√3 + 1) | = 50(√3 + 1) |
| √3 - 1 | (√3 - 1)(√3 + 1) | 3 - 1 |
Q14. From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 300 and 600 respectively. What is the height of the tower ?
(a) 45 m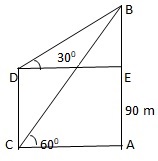
(b) 50 m
(c) 60 m
(d) 70 m
Answer: (c) 60 m
Let AB be the cliff and CD be the tower. Let DE || CA. Now ∠BDE = 300, ∠BCA = 600 and AB = 90 m
From Δ CAB we have
| CA | = Cot600 = | 1 |
| AB | √3 |
| ⇒ | CA | = | 1 |
| 90 | √3 |
| ⇒ CA = ( 90 X | 1 | X | √3 | ) = 30√3 m |
| √3 | √3 |
∴ DE = CA = 30√3 m
From Δ DEB,
| BE | = tan300 = | 1 |
| DE | √3 |
| ⇒ | BE | = | 1 |
| 30√3 | √3 |
| ⇒ BE = (30√3 X | 1 | ) = 30 m |
| √3 |
∴ CD = AE = AB - BE = 90 - 30 = 60 m
∴ Height of the tower = 60 m
Q15. If Sin 320 = x, then Cos 580 = ?
(a) x
(b) 1/x
(c) x2
(d) x3
Answer: (a) x
Cos 580 = Cos (902 - 322) = Sin 322 = x
Q16. Two men are opposite sides of a tower. They measure the angles of evaluation of the top of the tower as 300 and 450 respectively. If the height of the tower is 100 m, find the distance between the two men.
(a) 80(√2 + 1) m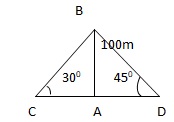
(b) 90(√3 + 1) m
(c) 100(√3 + 1) m
(d) 120(√5 + 1) m
Answer: (c) 100(√3 + 1) m
Let AB be the tower and let C and D be the positions of the two men. Then
∠ACB = 300, ∠ADB = 450, AB = 100 m
| AC | = Cot300 = √3 |
| AB |
| ⇒ | AC | = √3 |
| 100 |
⇒ AC = 100√3
| AD | = Cot450 = 1 |
| AB |
| ⇒ | AD | = 1 |
| 100 |
⇒ AD = 100 m
Distance between two men = CD = AC + AD = 100√3 + 100 = 100(√3 + 1) m
Q17. √(1+SinA)/(1-SinA) = ?
(a) SecA + SinA
(b) CosA + SinA
(c) SecA + tanA
(d) SecA + CosA
Answer: (c) SecA + tanA
√(1+SinA)/(1-SinA)
| = | √(1+SinA) |
| √(1-SinA) |
| = | √(1+SinA) . √(1+SinA) |
| √(1-SinA) . √(1+SinA) |
| = | (√(1+SinA))2 |
| √(1+SinA).(1-SinA) |
| = | √1+SinA |
| √1-Sin2A |
| = | 1+SinA | = | 1+SinA | = | 1 | + | SinA | = SecA + tanA |
| √Cos2A | CosA | CosA | CosA |
Q18. The angle of elevation of a ladder leaning against a wall is 450 and the foot of the ladder is 6m away from the wall. The length of the ladder is
(a) 4√2 m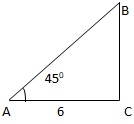
(b) 5√3 m
(c) 6√2 m
(d) 7√3 m
Answer: (c) 6√2 m
Let AB be the ladder leaning and CB be the wall.
Now AC = 6m
∠BAC = 450
| Now | AC | = Cos450 |
| AB |
| ⇒ | 6 | = 1/√2 |
| AB |
⇒ AB = 6√2 m
Q19. tan350tan400tan450tan500tan550 = ?
(a) 1
(b) 2
(c) 4
(d) 5
Answer: (a) 1
tan350tan400tan450tan500tan550
= tan350tan400tan450tan500tan(900 - 350)
= tan350tan400tan450tan500Cot350
= tan350tan400tan450tan5001/tan350
= tan400tan450tan(900 - 400)
= tan400tan450Cot400
= tan450 = 1
Q20. The shadow of a building is 20m long when the angle of elevation of the Sun is 450. Find the height of the building.
(a) 15 m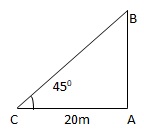
(b) 18 m
(c) 20 m
(d) 23 m
Answer: (c) 20 m
Let AB be the height and AC be the shadow of the building.
Now AC = 20 m
∠ACB = 450
| Now | AB | = tan450 |
| AC |
| ⇒ | AB | = 1 |
| 20 |
⇒ AB = 20 m

Practice Test Exam