Geometry - Quantitative Aptitude
Q21. Two poles of heights 5 m and 10 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops ?
(a) 13 cm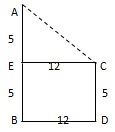
(b) 16 cm
(c) 19 cm
(d) 22 cm
Answer: (a) 13 cm
Let, AB abd CD be the poles.
Let AB = 10 m, CD = 5 m
BD = 12
AC = ?
We have AC2 = AE2 + EC2 = 52 + 122 = 169
∴ AC = √169 = 13 cm
Q22. The angles of a traingle are in the ratio 3 : 4 : 5. The measure of the bigger angle is
(a) 450
(b) 600
(c) 750
(d) 900
Answer: (c) 750
let the angles of the triangle be 3x, 4x, 5x
A/Q 3x + 4x + 5x = 1800
⇒ 12x = 1800
⇒ x = 150
∴ Bigger angle = 5 X 150 = 750
Q23. In Δ ABC, ∠A + ∠B = 550 and ∠B + ∠C = 1500, then ∠B = ?
(a) 250
(b) 300
(c) 450
(d) 500
Answer: (a) 250
We have ∠A + ∠B + ∠C = 1800
⇒ 550 + ∠C = 1800
⇒ ∠C = 1800 - 550 = 1250
Now ∠B + ∠C = 1500
⇒ ∠B = 1500 - ∠C = 1500 - 1250 = 250
Q24. The lengths of the diagonals of a rhombus are 24 cm and 18 cm respectively. The length of each side of the rhombus is
(a) 10 cm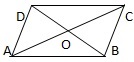
(b) 15 cm
(c) 18 cm
(d) 23 cm
Answer: (b) 15 cm
Let, ABCD be the rhombus
Let AC = 24 cm, BD = 18 cm
Now OA = ½ AC = ½ X 24 = 12 cm
OB = ½ BD = ½ X 18 = 9 cm
AB2 = AO2 + OB2 = 122 + 92 = 144 + 81 = 225
∴ AB = √225 = 15 cm
Q25. An angle is 300 less than its supplement. The measure of the angle is
(a) 250
(b) 450
(c) 750
(d) 900
Answer: (c) 750
Let the angle be x0
∴ Suppliment angle = x0 + 300
A/Q x + x + 300 = 1800
⇒ 2x = 1800 - 300 = 1500
⇒ x = 750
Q26. An angle is 100 more than its complement. The measure of the angle is
(a) 400
(b) 450
(c) 500
(d) 650
Answer: (c) 500
Let the angle be x0
∴ Complement angle = x0 - 100
A/Q x + x - 100 = 900
⇒ 2x = 1000
⇒ x = 500
Q27. In the given figure, AOB is a diameter of the circle and CD || AB. If ∠CAB = 250, then ∠CAD = ?
(a) 250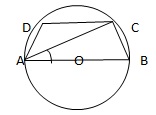
(b) 400
(c) 450
(d) 600
Answer: (b) 400
AB || CD, AC transversal
∴ ∠ACD = ∠CAB = 250
∠ACB = 900 (Same circular angle)
∴ ∠BCD = ∠ACB + ∠ACD = 900 + 250 = 1150
∠BAD + ∠BCD = 1800
⇒ ∠BAC + ∠CAD + ∠BCD = 1800
⇒ 250 + ∠CAD + 1150 = 1800
⇒ ∠CAD = 400
Q28. In a Δ ABC, AB =BC, ∠B = x0 and ∠A = (2x - 20)0 then ∠B = ?
(a) 150
(b) 280
(c) 440
(d) 560
Answer: (c) 440
AB = BC
⇒ ∠A = ∠C
⇒ ∠C = (2x - 20)0
A/Q x0 + (2x - 20)0 + (2x - 20)0 = 1800
⇒ 5x = 2200
⇒ x = 440

Practice Test Exam