Co-ordinate Geometry - Quantitative Aptitude
Q11. The vertices of a Δ ABC are A (-8, 5), B (-3, 0) and C(5, 2). The centroid of Δ ABC is
(a) (-2, 5/3)
(b) (-2, 7/3)
(c) (-3, 5/3)
(d) (-3, 7/3)
Answer: (b) (-2, 7/3)
Here x1 = -8 x2 = -3 x3 = 5
y1 = 5 y2 = 0 y3 = 2
∴ centroid = {1/3(x1+x2+x3), 1/3(y1+y2+y3)}
= {1/3(-8 - 3 + 5), 1/3(5 + 0 + 2)}
= {1/3(-6), 1/3(7)}
= (-2, 7/3)
Q12. The slope of a line passing through the points A (6, -4) and B (5, -2) is
(a) -2
(b) -1
(c) 1
(d) 2
Answer: (a) -2
Here x1 = 5 x2 = 6
Here y1 = -2 y2 = -4
| ∴ Slope = | y2 - y1 | = | -4 - (-2) | = | -2 | = -2 |
| x2 - x1 | 6 - 5 | 1 |
Q13. P is a point on y-axis at a distance of 4 units from x-axis lying below x-axis. The Co-ordinate of A are
(a) (0, -3)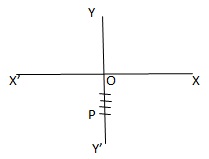
(b) (0, -4)
(c) (1, -3)
(d) (2, -4)
Answer: (b) (0, -4)
Q14. The equation of a line passing through the points A (-2, 1) and B (3, -4) is
(a) 0
(b) 2
(c) 3
(d) 4
Answer: (a) 0
Here x1 = -2 x2 = 3
y1 = 1 y2 = -4
The equation of the line is
| y - y1 | = | y2 - y1 |
| x - x1 | x2 - x1 |
| ⇒ | y - 1 | = | - 4 - 1 |
| x + 2 | 3 + 2 |
| ⇒ | y - 1 | = | - 5 | = - 1 |
| x + 2 | 5 |
⇒ y - 1 = -x - 2
⇒ x + y + 1 = 0
Q15. Two vertices of a Δ PQR are Q (0, -2), R (-3, 1) and its centroid is at the origin. The third vertex P is
(a) (2, 1)
(b) (2, 3)
(c) (3, 1)
(d) (4, 1)
Answer: (c) (3, 1)
Let P be (x, y)
Now x1 = 0 x2 = x x3 = -3
y1 = -2 y2 = y y3 = 1
A/Q 1/3 (x1 + x2 + x3) = 0
⇒ 1/3 (0 + x - 3) = 0
⇒ x - 3 = 0
⇒ x = 3
Also 1/3 (y1 + y2 + y3) = 0
⇒ 1/3 (-2 + y + 1) = 0
⇒ - 1 + y = 0
⇒ y = 1
∴ P is (3, 1)
Q16. If the points x (1, -1), y (k, 5) and z (5, 2) are co-linear then k = ?
(a) 3
(b) 5
(c) 7
(d) 9
Answer: (d) 9
Here x1 = 1 x2 = k x3 = 5
y1 = -1 y2 = 5 y3 = 2
Now Δ = {x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)}
⇒ 0 = 1 (5 - 2) + k (2 + 1) + 5 (-1 - 5)
⇒ 0 = 3 + 3k - 30
⇒ 3k = 27
⇒ k = 9
Q17. The value of k for which the lines 4x + ky + 8 = 0 and 25x - 16y + 23 = 0 are perpendicular to each other is
(a) 21/7
(b) 25/4
(c) 29/7
(d) 35/4
Answer: (b) 25/4
25x - 16y + 23 = 0
⇒ -16y = -25x - 23
| ⇒ y = | -25 | x - | 23 |
| -16 | -16 |
| = | 25 | x + | 23 |
| 16 | 16 |
∴ m1 = 25/16
4x + ky + 8 = 0
⇒ ky = -4x - 8
| ⇒ y = | -4 | x - | 8 |
| k | k |
m2 = -4/k
The lines are perpendicular
∴ m1 . m2 = -1
| ⇒ | 25 | . | - 4 | = - 1 |
| 16 | k |
⇒ 25/4k = 1
⇒ k = 25/4
Q18. Find the co-ordinates of a point P which divides the joint of A (5, -2) and B (8, 6) in the ratio 3:2 ?
(a) (22/5 , 11/5)
(b) (27/5 , 13/5)
(c) (34/5 , 14/5)
(d) (39/5 , 16/5)
Answer: (c) (34/5 , 14/5)
Here x1 = 5 x2 = 8
y1 = -2 y2 = 6
m = 3
n = 2
| ∴ P is ( | mx2 + nx1 | , | my2 + ny1 | ) |
| m + n | m + n |
| = ( | 3 X 8 + 2 X 5 | , | 3 X 6 + 2 X (-2) | ) |
| 3 + 2 | 3 + 2 |
| = ( | 34 | , | 14 | ) |
| 5 | 5 |
Q19. Y-axis divides the join of P (-4, 2) and Q (8, 3) in the ratio
(a) 1 : 2
(b) 1 : 3
(c) 2 : 3
(d) 3 : 5
Answer: (a) 1 : 2
Let the required ratio be m : 1
| Its co-ordinate = ( | 8m - 4 | , | 3m + 2 | ) |
| m + 1 | m + 1 |
But it lies on y-axis
| ∴ | 8m - 4 | = 0 |
| m + 1 |
⇒ 8m - 4 = 0
⇒ 8m = 4
⇒ m = ½
Required ratio ½ : 1 = 1 : 2
Q20. A line passes through the point (3, 5) and makes an angle 1350 with the x-axis. The equation of the line is
(a) x + y + 8 = 0
(b) x + y - 8 = 0
(c) x - y - 8 = 0
(d) x - y + 8 = 0
Answer: (b) x + y - 8 = 0
The equation of the line is
| y - 5 | = tan 1350 |
| x - 3 |
| ⇒ | y - 5 | = tan (1800 - 450) = -tan 450 = -1 |
| x - 3 |
⇒ y - 5 = -x + 3
⇒ x + y - 8 = 0

Practice Test Exam