Quantitative Aptitude on Times and Distance
Q31. By how much percent must a motorist increases his speed in order to reduce the time by 10%, taken to cover a certain distance ?
(a) 101/9 %
(b) 111/9 %
(c) 134/9 %
(d) 145/9 %
Answer: (b) 111/9 %
Let the required increase in speed be P %
| Then 90% of time X | 100 + P | X speed = time X speed |
| 100 |
| ⇒ | 90 | X time X | 100 + P | X speed = time X speed |
| 100 | 100 |
| ⇒ | 90(100 + P) | = 1 |
| 100 X 100 |
⇒ 900 + 9P = 1000
⇒ 9P = 100
⇒ p = 100/9 = 111/9 %
Q32. A car covers four successive 2 km stretches at 20 km/hr, 30 km/hr, 40 km/hr and 60 km/km respectively. Its average speed over this distance is
(a) 22 km/hr
(b) 25 km/hr
(c) 29 km/hr
(d) 32 km/hr
Answer: (d) 32 km/hr
Total distance = 2 X 4 km = 8 km
| Total time taken = ( | 2 | + | 2 | + | 2 | + | 2 | ) h |
| 20 | 30 | 40 | 60 |
| = | 12 + 8 + 6 + 4 | h |
| 120 |
| = | 30 | h |
| 120 |
| = | 1 | h |
| 4 |
| Average speed = | 8 | km/h = 32 km/h |
| 1/4 |
Q33. A car travels a distance of 840 km at a uniform speed. If the speed of the car is 10 km/h more, it takes 2 hours less to cover the same distance. The original speed of the car was
(a) 53 km/hr
(b) 57 km/hr
(c) 60 km/hr
(d) 63 km/hr
Answer: (c) 60 km/hr
Let, the original speed of the car be x km/hr
| A/Q | 840 | = 2 + | 840 |
| x | x + 10 |
| ⇒ | 840 | = | 2x + 20 + 840 |
| x | x + 10 |
⇒ 840x + 8400 = 2x2 + 860x
⇒ 2x2 + 20x - 8400 = 0
⇒ x2 + 10x - 4200 = 0
⇒ x2 + 70x - 60x - 4200 = 0
⇒ x (x + 70) - 60 (x + 70) = 0
⇒ (x + 70) (x - 60) = 0
∴ x = 60 km/h
Q34. The ratio between the rates of walking of x and y is 3:4, If the time taken by x to cover a certain distance is 36 minutes, the time taken by Y to cover the certain distance is
(a) 25 minutes
(b) 27 minutes
(c) 32 minutes
(d) 35 minutes
Answer: (b) 27 minutes
| Ratio of the time taken by x and y = | 1 | : | 1 | = 4 : 3 |
| 3 | 4 |
Let, the time taken by x and y be 4x and 3x minutes
A/Q 4x = 36
⇒ x = 9
∴ time taken by y = 3 X 9 minutes = 27 minutes
Q35. A plane left 30 minutes later than the scheduled time and in order to reach the destination 1500 km away in time, it had to increase the speed by 250 km/hr from the usual speed. Its ususal speed is
(a) 478 km/h
(b) 550 km/h
(c) 600 km/h
(d) 750 km/h
Answer: (d) 750 km/h
Let, the usual speed be x km/hr
| A/Q | 1500 | - | 1500 | = | 1 |
| x | x + 250 | 2 |
| ⇒ | 1 | - | 1 | = | 1 |
| x | x + 250 | 3000 |
| ⇒ | x + 250 - x | = | 1 |
| x (x + 250) | 3000 |
| ⇒ | 250 | = | 1 |
| x (x + 250) | 3000 |
⇒ x2 + 250x - 750000 = 0
⇒ x2 + 1000x -750x - 750000 = 0
⇒ x (x + 1000) - 750 (x + 1000) = 0
⇒ (x + 1000) (x - 750) = 0
∴ x = 750 km/h
Q36. Two cars starts at the same time from one point and move along two roads at right angles to each other. Their speeds are 18 km/hr and 36 km/hr respectively. After 10 seconds the distance between them will be
(a) 48√5 m
(b) 50√5 m
(c) 53√5 m
(d) 55√5 m
Answer: (b) 50√5 m
| 18 km/h = | 18000 m | = 5 m/sec |
| 60 X 60 sec |
| 36 km/h = | 36000 m | = 10 m/sec |
| 60 X 60 sec |
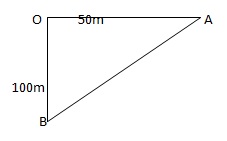
Distance covered in 10 sec OA = 5 X 10 m = 50 m
Distance covered in 10 sec OB = 10 X 10 m = 100 m
Now AB = √(OA2 + OB2) = √(502 + 1002) = √(2500 + 10000) = √12500 = 50√5 m
Q37. A man on tour travels first 150 km at 55 km/hr and the next 150 km at 65 km/hr. The average speed of the whole journey is
(a) 57.48 km/hr
(b) 57.82 km/hr
(c) 58.12 km/hr
(d) 59.58 km/hr
Answer: (d) 59.58 km/hr
| Average speed = | 2xy | km/hr |
| x + y |
| = | 2 X 55 X 65 | km/hr |
| 55 + 65 |
| = | 2 X 55 X 65 | km/hr |
| 120 |
| = | 55 X 65 | km/hr |
| 60 |
= 59.58 km/hr
Q38. Ram has to cover 8 km in 45 minutes. If he covers one half of the distance in 1/3 rd of time, what should be his speed to cover the remaining distance in the remaining time
(a) 6 km/hr
(b) 7 km/hr
(c) 8 km/hr
(d) 9 km/hr
Answer: (c) 8 km/hr
| Time left = ( | 2 | X 45) minutes = 30 minutes = ½ h |
| 3 |
Distance left = 8 X ½ = 4 km
∴ Required Speed = (4 ÷ ½ ) km/h = 8 km/hr
Q39. In what time can Naren cover a distance of 500 m, if he runs at a speed of 25 km/hr
(a) 11/5 minutes
(b) 21/3 minutes
(c) 21/5 minutes
(d) 31/5 minutes
Answer: (a) 11/5 minutes
| Distance = 500 m = | 500 | km = ½ km |
| 1000 |
Speed = 25 km/hr
| ∴ Time = | ½ km | = | 1 | hr = | 60 | minutes = 1 | 1 | minutes |
| 25 km/hr | 50 | 50 | 5 |
Q40. The distance between two stations A and B is 200 km. A train leaves A towards B at 80 km/hr. After half an hour, another train leaves B towards A at 100 km/hr. The distance of the point where the two trains meet, from A is
(a) 111.11 km
(b) 112.22 km
(c) 112.25 km
(d) 115.55 km
Answer: (a) 111.11 km
Let the required distance be x km
| A/Q | x | - | 200 - x | = ½ |
| 80 | 100 |
| ⇒ | 5x - 800 + 4x | = ½ |
| 400 |
⇒ 9x - 800 = 200
⇒ 9x = 1000
⇒ x = 111.11 km

Practice Test Exam